728x90

안녕하세요 뚜디 입니다:)
다변수 선형 회귀(Multi-variable Linear Regression)를 tensorflow 코드로 어떻게 구현하는지 살펴보도록 하겠습니다.

변수(x1,x2,3)이므로 weight도 세개가 되는 hypothesis를 확인하실수 있습니다.
x1,x2,x3 : 입력 데이터 / y : 출력 데이터 (정답,예측값)
를 통해 훈련한 다음에 나중에 새로운 데이터 x1,x2,x3가 왔을 때 어떤값이 나올지를 예측(y)를 하게됩니다.
Multi-variable Linear Regression을 표현
import numpy as np
import tensorflow as tf
x1 = [73., 93., 89., 96., 37.]
x2 = [80., 88., 91., 98., 66.]
x3 = [75., 93., 90., 100., 70.]
y = [152., 185., 180., 196., 142.]
w1 = tf.Variable(tf.random.normal([1]))
w2 = tf.Variable(tf.random.normal([1]))
w3 = tf.Variable(tf.random.normal([1]))
b = tf.Variable(tf.random.normal([1]))
learning_rate = 0.000001
for i in range(1000+1):
with tf.GradientTape() as tape:
hypothesis = w1 * x1 + w2 * x2 + w3 * x3 + b
cost = tf.reduce_mean(tf.square(hypothesis - y))
w1_grad, w2_grad, w3_grad, b_grad = tape.gradient(cost, [w1, w2, w3, b])
w1.assign_sub(learning_rate * w1_grad)
w2.assign_sub(learning_rate * w2_grad)
w3.assign_sub(learning_rate * w3_grad)
b.assign_sub(learning_rate * b_grad)
if i % 100 == 0:
print("{:5} | {:12.4f}".format(i, cost.numpy()))
해당 소스 코드는 simple linear regression을 하는 과정에서 조금 변형한 과정입니다.
Gradient descent를 통해서 weight값을 지속적으로 업데이트 해나가는 내용
결과를 살펴보게되면,
i 값이 증가할때 cost 값을 보게되면 일정 정도 줄어든 상태에서는 cost값이 크게 줄지 않는 모습을 보이고 있다.
Multi-variable Linear Regression을 Matrix로 표현

Matrix를 사용하게되면 훨씬 간결하게 표현할 수 있다.
X = data[:, :-1]는 numpy의 slicing을 활용해서 데이터를 잘라내는 것 = ( data['행', '열']로 구분한다. )
-> row는 전체를 뜻하고, column은 마지막을 제외한 전체를 뜻한다.
Y = data[:, [-1]]
-> row는 전체를 뜻하고, column은 마지막 column을 뜻한다.
W(weight Matrix)는 X[5X3], Y[5X1] 이므로 X[5X3] * W[?X?] = Y[5X1] 따라서 W[3X1]을 갖게된다.
W = tf.Variable(tf.random.normal([3, 1]))을 선언
가설 함수(hypothesis)는 H= XW이므로 tf.matmul(X,W) + b 여기서 b는 생략가능
import numpy as np
import tensorflow as tf
def predict(X):
return tf.matmul(X, W) + b
data = np.array([
[73., 80., 75., 152.],
[93., 88., 93., 185.],
[89., 91., 90., 180.],
[96., 98., 100., 196.],
[73., 66., 70., 142.]
], dtype=np.float32)
X = data[:, :-1]
y = data[:, [-1]]
W = tf.Variable(tf.random.normal([3, 1]))
b = tf.Variable(tf.random.normal([1]))
learning_rate = 0.000001
n_epochs = 2000
for i in range(n_epochs+1):
with tf.GradientTape() as tape:
cost = tf.reduce_mean(tf.square(predict(X) - y))
W_grad, b_grad = tape.gradient(cost, [W, b])
W.assign_sub(learning_rate * W_grad)
b.assign_sub(learning_rate * b_grad)
if i % 100 == 0:
print("{:5} | {:10.4f}".format(i, cost.numpy()))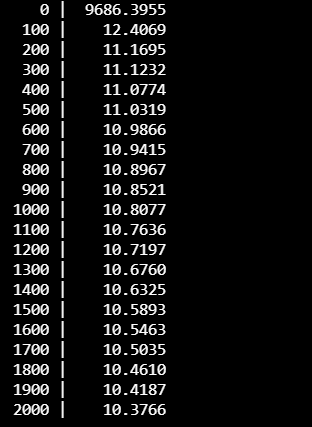
Multi-variable Linear Regression을 Matrix로 구현한 코드에서 마찬가지로
i 값이 증가할때, cost값이 변화는것을 확인할 수 있다.
Matrix를 사용했을 때와 안했을때의 차이

728x90
'Machine Learning > Basic Machine Learning' 카테고리의 다른 글
| [ML/DL] 로지스틱 회귀/분류 (Logistic Regresion/Classification) (0) | 2022.01.21 |
|---|---|
| [ML/DL] 다변수 선형 회귀 분석 Multi-variable Linear Regression (0) | 2022.01.19 |
| [ML/DL] 선형 회귀 분석 및 비용 최소화 방법(2) (0) | 2021.10.29 |
| [ML/DL] 선형 회귀 분석 및 비용 최소화 방법 (0) | 2021.10.19 |
| [ML/DL] 선형회귀(Linear Regression)를 TensorFlow로 구현하기 (0) | 2021.10.18 |



